算法复杂度

算法是指用来操作数据、解决程序问题的一组方法，而算法复杂度是考评算法执行效率和资源消耗的一个重要指标。

算法优劣主要从「时间」和「空间」两个维度去考量。

时间维度：是指执行当前算法所消耗的时间，我们通常用「时间复杂度」来描述。
空间维度：是指执行当前算法需要占用多少内存空间，我们通常用「空间复杂度」来描述。

在符合算法本身的要求的基础上，编写的程序运行时间越短，运行过程中占用的内存空间越少，意味着这个算法越“好”。

时间复杂度

时间复杂度是描述算法运行的时间。我们把算法需要运算的次数用输入大小为 $ n $ 的函数来表示，计作 $ T(n) $。时间复杂度通常用 $ O(n) $ 来表示，公式为 $ T(n)=O(f(n)) $，其中 $ f(n) $ 表示每行代码的执行次数之和，注意是执行次数。

常见的时间复杂度

名称	运行时间 $ T(n) $	时间举例	算法举例
常数	$ O(1) $	$ 1 $	加法运算
线性	$ O(n) $	$ n $	数组遍历
平方	$ O(n^2) $	$ n^2 $	冒泡排序
立方	$ O(n^3) $	$ n^3 $	矩阵乘法
对数	$ O(log(n)) $	$ log(n) $	二分搜索
线性对数	$ O(nlog(n)) $	$ nlog(n) $	比较排序

常数的时间复杂度 $ O(1) $

算法执行所需要的时间不随着某个变量 $ n $ 的变化而变化，即此算法时间复杂度为一个常量，可表示为 $ O(1) $。

比如，最常见的加法运算：

const sum = 1 + 2

上述代码在执行的时候，它执行所需的时间并不随着某个变量 $ n $ 的变化而变化，这类代码即便有几十万行，都可以用 $ O(1) $ 来表示它的时间复杂度。

线性的时间复杂度 $ O(n) $

for (let i = 0; i < n; i++) {
  console.log(i)
}

for 循环里面的代码会执行 $ n $ 次，因此它执行所需时间是随着 $ n $ 的变化而变化，因此得到复杂度为 $ O(n) $。

平方的时间复杂度 $ O(n^2) $

for (let i = 0; i < n; i++) {
  for (let j = 0; j < n; i++) {
    console.log(i, j)
  }
}

上述代码存在两个循环，外层需要执行 $ n $ 次，内层也需要执行 $ n $ 次，它的时间复杂度就是 $ O(n * n) $，即 $ O(n^2) $。

对数的时间复杂度 $ O(log(n)) $

在数学中，对数是幂运算的逆运算。换句话说，假如 $ x = \beta^y $，则有 $ y = log_\beta x $，其中 $ \beta $ 是对数的底（也称为基数），而 $ y $ 就是 $ x $（对于底数 $ \beta $ ）的对数。

let i = 1
while(i <= y) {
  i *= 2
}

对数复杂度 $ O(log(n)) $ 是比较常见的一种复杂度，也是比较难分析的一种复杂度。观察上面的代码， $ i $ 从 1 开始，每循环一次就乘以 2，直到 $ i $ 大于 $ n $ 时结束循环。

$$ 2^1 -> 2^2 -> 2^3 -> … -> 2^x $$

观察上面列出 $ i $ 的取值发现，是一个等比数列，要知道循环了多少次，求出 $ x $ 的值即可。由 $ 2^x = n $ 得到 $ x = log_2 n $，所以这段代码的时间复杂度为 $ log_2 n $。

如果把上面的 i *= 2 改为 i *= 3，那么这段代码的时间复杂度就是 $ log_3 n $。

根据换底公式：

$$ log_c a * log_a b = log_c b $$

因此 $ log_3 n = log_3 2 * log_2 n $，其中 $ log_3 2 $ 是一个常量，得到 $ O(log_3 n) = O(log_2 n) $。当我们忽略对数的“底”之后，我们可以获得 $ O(log(n)) $ 的复杂度。

递归的时间复杂度

我们在面试的时候，经常会被问及递归的概念，那么递归的时间复杂度如何计算呢？

递归算法中，每个递归函数的的时间复杂度为 $ O(s) $，递归的调用次数为 $ n $，则该递归算法的时间复杂度为 $ O(n) = n * O(s) $，其中 $ O(s) $ 可能是任意的时间复杂度。因此，我们可以认为递归的时间复杂是一个复合型的时间复杂度。

我们以经典的斐波那契数列（Fibonacci sequence）为例：

$$ F(0) = 1, F(1) = 1, F(n) = F(n−1) + F(n−2)(n ≥ 2, n \in N ∗) $$

function fibonacci(n) {
  if (n === 0 || n === 1) return 1
  return fibonacci(n - 1) + fibonacci(n - 2)
}

我们很容易写出上面这样一段递归的代码，往往会忽略了时间复杂度是多少，换句话说调用多少次。可以代一个数进去，例如 n = 5，完了之后大概就能理解递归的时间复杂度是怎么来的。

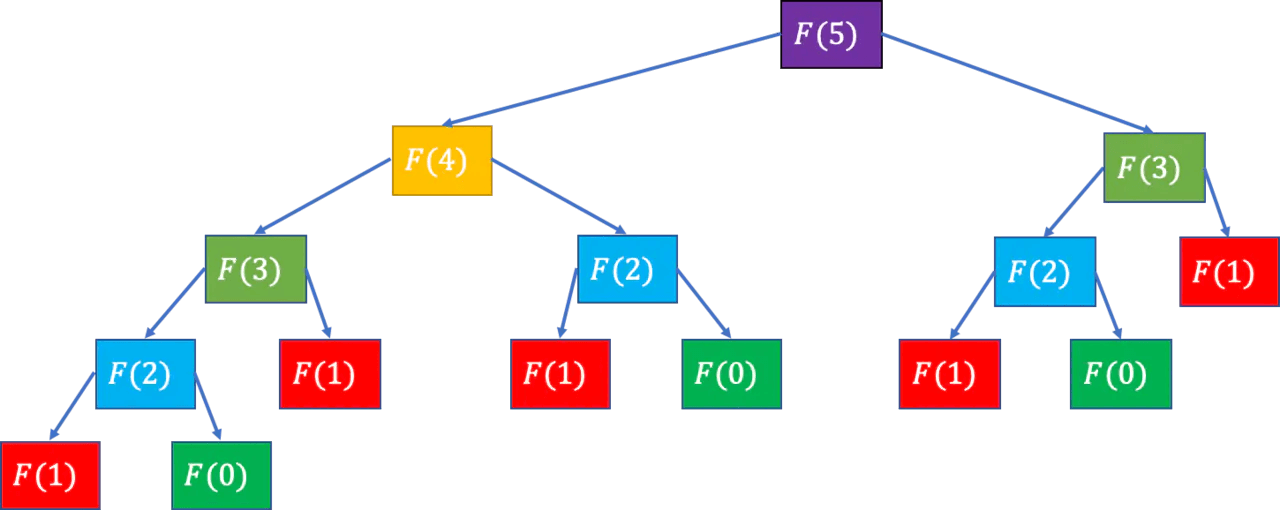
上图把 n = 5 的情况都列举出来。可以看出，虽然代码非常简单，在实际运算的时候会有大量的重复计算。

在 $ n $ 层的完全二叉树中，节点的总数为 $ 2^n - 1 $，所以得到 $ F(n) $ 中递归数目的上限为 $ 2^n - 1 $。因此我们可以毛估出 $ F(n) $ 的时间复杂度为 $ O(2^n) $。

时间复杂度为 $ O(2^n) $，指数级的时间复杂度，显然不是最优的解法。

// 黄金分割率
const goldenRatio = (1 + Math.sqrt(5)) / 2
function fibonacci(n) {
  return Math.round((Math.pow(goldenRatio, n - 1) + Math.pow(goldenRatio, n)) / Math.sqrt(5))
}

以上写法是借助了斐波那契数列和黄金分割的关系，开普勒发现数列前、后两项之比 1/2, 2/3, 3/5, 5/8, 8/13, 13/21, 21/34 …，也组成了一个数列，会趋近黄金分割：

$$ \frac{f_{n+5}}{f_n} \approx a = \frac{1}{2}({1 + \sqrt{5}}) = \varphi \approx 1.6180339887… $$

因此，我们可以认为黄金分割率 $ \varphi $ 是一个常数，因此该算法的时间复杂度为 $ O(1) $。

空间复杂度

空间复杂度是对算法运行过程中临时占用空间大小的度量，也是一种趋势。一个算法所需的存储空间用 $ f(n) $ 表示，可得出 $ S(n) = O(f(n)) $，其中 $ n $ 为问题的规模，$ S(n) $ 表示空间复杂度。

$ O(1) $ 复杂度

如果算法执行所需要的临时空间不随着某个变量 $ n $ 的大小而变化，即此算法空间复杂度为一个常量，可表示为 $ O(1) $。

const i = 1
const j = 2

上述代码，执行所需要的临时空间不会随着处理数据量的变化而变化，因此得到空间复杂度为 $ O(1) $。

$ O(n) $ 复杂度

const arr = new Array(n)
for (let i = 0; i < n; i++) {
  console.log(arr[i])
}

上述代码一开始申请了长度为 $ n $ 的数组空间，但之后的 for 循环中没有分配新的空间，可以得出这段代码的时间复杂度为 $ O(n) $，即 $ S(n) = O(n) $。

时间空间相互转换

对于一个算法来说，它的时间复杂度和空间复杂度往往是相互影响的。

那我们熟悉的 Chrome 来说，流畅性方面比其他厂商好了多人，但是占用的内存空间略大。

当追求一个较好的时间复杂度时，可能需要消耗更多的储存空间。 反之，如果追求较好的空间复杂度，算法执行的时间可能就会变长。

总结

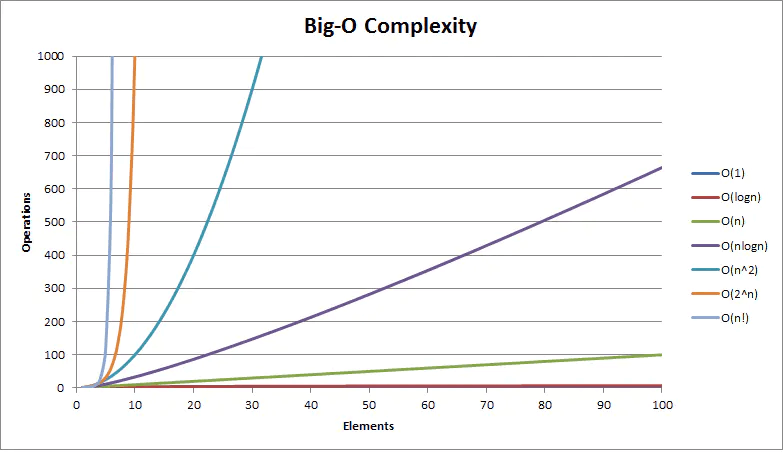
常见的复杂度不多，从低到高排列就这么几个：$ O(1) $、$ O(log(n)) $、$ O(n) $、$ O(n^2) $，很多算法题涉及的算法复杂度也基本上只有这几种。

参考文献

• 算法 101
• 算法的时间与空间复杂度

此为原创文章，转载请注明出处